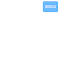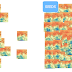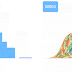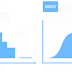
Imagine a game board and try to get "boundary condition"...
 where:
where:- blue arrows shows "far left" and "far right" cases;
- red arrows shows situation that will never happend (probability 0).
Also imagine "missing of a peg" situation,
 where:
where:- blue arrows shows that ball goes forward to the bottom with the same probability as it has before.
Test case from problem description

1st test case from example input











15 comments:
Thanks ! This is the only correct interpretation of the problem ! in my opinion =)
This is my interpretation of the problem as well. I dislike the angled boundaries, but given the math provided plus sample problems/solutions, it's the only thing that makes sense.
Hopefully the next round will be more clear.
Dear Illya Havsiyevych,
What about the second test case in the given example? I think I coded based on same strategy with yours, but, in my case, the probability is 0.5 when starting point is 1 and 2.
According to the problem, there is no ties or near. I did it several time on paper also, but I got same result.
Could you kindly explain what I might be missing?
I didn't exactly get that result. Instead of doing it your method I took out the peg at (2,2). I did manage to get the problem correct but it required doing a perfect grid ie:
x.x.x.x
x.x.x.x
x.x...x
x.x.x.x
x.x.x.x
#1pos: (0,0)
#2pos: (1,1) 1.0 probability
#3pos: (2,0).5prob (2,2).5prob
#4pos: (3,1).75prob (3,3).25prob
#5pos: (4,0).375prob (4,2).3125prob
leaving the ball in the first column (0) at .375000 probability. The reason at position 3 the ball goes to 2,2 then to 3,3 is because the peg is missing.
I would like to introduce the following pseudo-code to present my findings:
for(rows)
#1(0,0) = 1.0
//if(col = 0) then increment and keep probability
#2(1,1) = 1.0/2 //column not 0
//peg splits and col +- 1
#3(2,0) = .5 and (2,2) = .5
#4(3,1) = .5/2 and (3,2) = .5/2 //peg missing
#5(4,0) = .25 and (4,1) = .25/2 and (4,3) = .25/2
//if(col0 and col1 exists)
#6(END) = .25+.125=.375
FYI, my output for input file
-----------------------------
48 0.112857
0 0.375000
0 0.500000
16 0.089765
24 0.100113
8 0.175087
2 0.250000
35 0.230835
0 1.000000
25 0.089105
9 0.124782
8 0.167464
52 0.101299
30 0.100734
17 0.214032
44 0.266663
85 0.511620
11 0.072748
5 0.359375
2 1.000000
Can you give your input file... Just for testing purpose...
I am not sure your output is right... I got a different one...
Be careful, he is trying to decieve you! His solution is nowhere right, because 15th test case is 4 3 0 0, and his output is 17 column which does not even exist!
Please ignore my output because it looks like it has no sense without input. So some cases from my input:
2nd:
5 4 0 1 2 2
3rd:
3 4 0 0
7th:
5 4 2 6 1 1 3 0 2 0 2 3 3 1 1 0
9th:
3 3 0 1 1 0
15th:
71 35 17 1191 ....
Post a Comment